Numerical Analysis Labs Explained

Eight labs in total, covering basic calculation with acdelerated convergence, interpolation, approximation, numerical differentiation and integration, solving linear equations, factorization, eigenvalue problems, etc.
Language is restricted to C, for libraries for data processing in other languages are not allowed, after all, these libraries sacrifice flexibility for convenience.
You can find my source code here

Lab 1

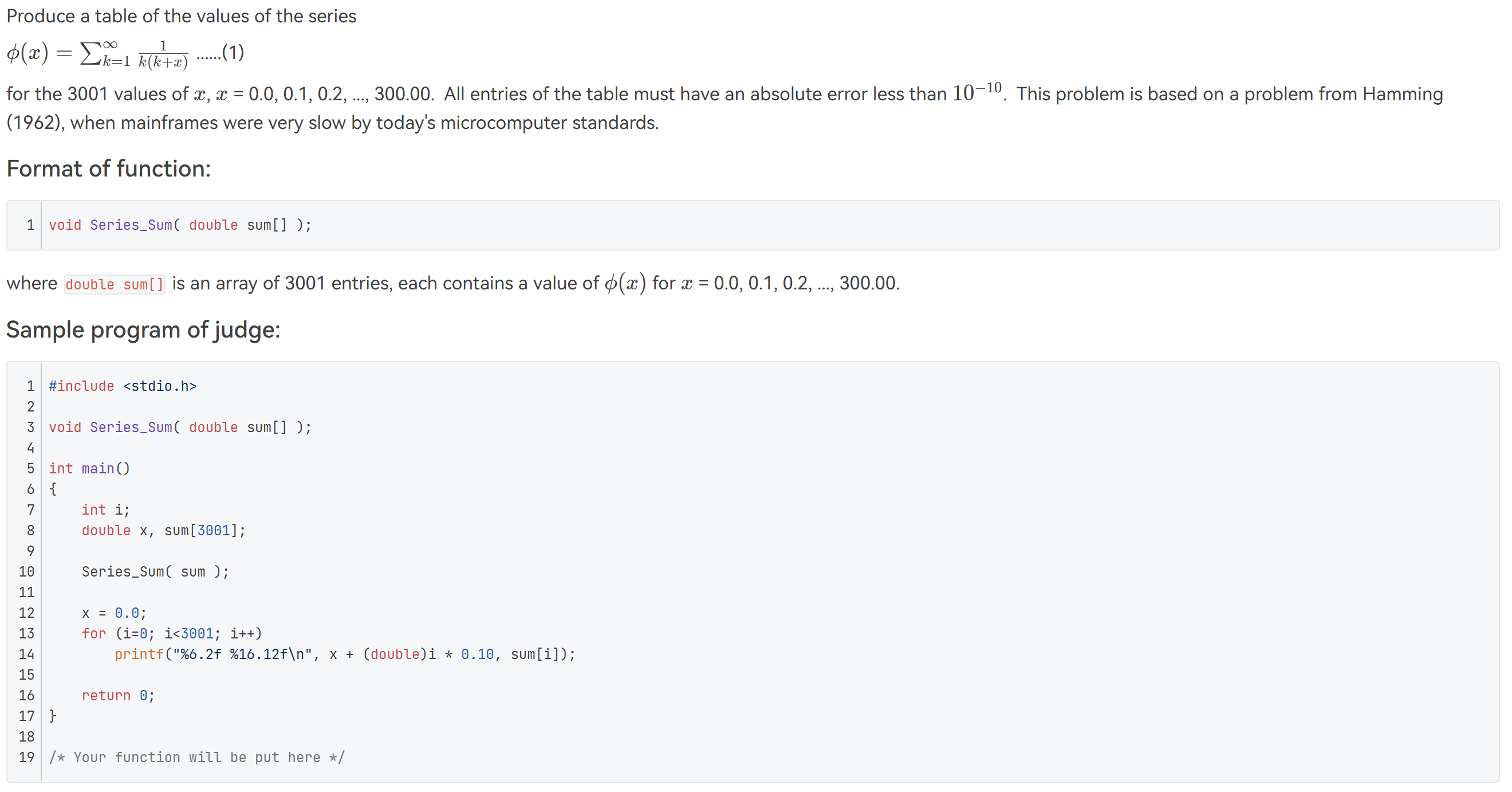
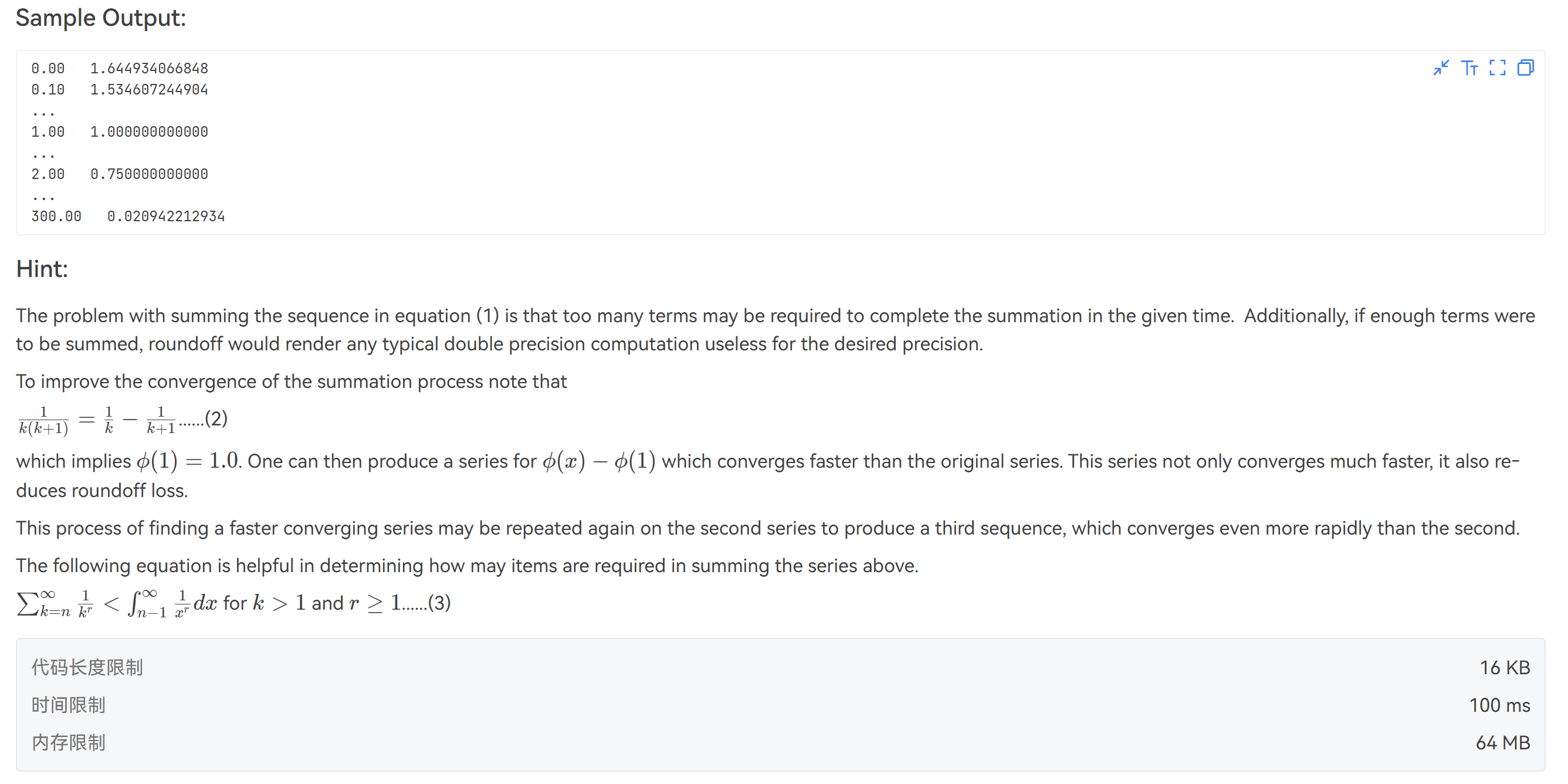
HINT: Since computers were not that powerful in the past, the calculation of a series was a big deal. Time complexity and rounding errors are the two main concerns. Therefore, we need to find a way to accelerate the convergence of the series.

To make this $\sum_{k=1}^{\infty}\frac{1}{k(k+1)}$ converge faster, we need dominator exponent of $k$ as large as possible, without losing any accuracy.

We can acquire the precise result of the progression when $x$ is an interger. Therefore, we may multiply $k+t$ when $t\in N$ to both the numerator and the dominator, then seperate the series into various parts. I suggest $t$ has a relationship with the specific $x$, personally I prefer $t=\lfloor x \rfloor$. Then you may acquire a remain unsolved series, and some series that can be calculated precisely, with their x being integers. The dominator of the unsolved series must have a exponent of $k$ larger or equal to 4. Then apply loops to solve the series.